Having explored the racecar project for far too long, I wanted to work on something different that could offer newer challenges. I’ve always wanted to build a game-playing RL agent for complex games like modern boardgames but those still seem too complicated for me right now. I needed something of a stepping stone before I could get there.

The classic Connect-4 game has been a personal obsession of mine at various points in my life. It was my first glorious “AI” game when I used a brute-force recursive lookahead to optimize moves. At 15, this was a big deal for me! Many years later I heard that researchers had been able to completely “solve” the game to play perfectly, and I was obsessed with wanting to precompute this entire game-tree – on a single computer within a reasonable timeframe. I eventually coded this up, a perfect-playing agent that would never lose a game (as long as it played first). The precomputation took only about 2 weeks to run on a single computer with 16GB RAM.

Reinforcement learning of Connect-4  differs from the racecar project in several interesting ways:

• Intuitively, games like Connect-4 (and checkers and chess) involve “lookahead”. As human players, we take the time to foresee and plan for future moves. So, without lookahead, it’s not at all clear whether value function approximators (even deep neural networks) can capture that lookahead logic within “experience-based hunches”. I’m curious about this.
• Rewards are only handed out at the end of the episode in the form of a win/lose/draw.
• As a 2-player game, the agent performance depends on the strength of its opponents. So, it is not obvious what training ‘regimen’ will work best – whether the agent should be matched against opponents that are equally-skilled or those that are stronger. In addition, there is the tantalizing possibility of training the agent against itself.
• While racecar actions were mostly deterministic, Connect-4 actions have much greater environmental unpredictability, i.e. when an action is perfomed, the resulting state depends very much on how the opponent chooses to respond.
• The total number of connect-4 states is too big to attempt a full-state table-lookup. Function approximators become a necessity.
• Similarly, exploration may be complicated since it’s no longer possible to keep track of the number of visits to every state.
• It may further be worthwhile to try modeling the opponent’s behavior explicitly (but I won’t be pursuing that option for now)

At the same time, Connect-4 is not as complex as a modern boardgame might be:

• The length of an episode is between 7 and 42 steps, which is quite small and on a similar scale as the (juncture-based) racecar.
• The number of possible actions at every state is similarly small, at just 7.
• There is no hidden state to worry about. The opponent has no hidden cards. It isn’t important to get into the opponent’s head.
• The game rules/mechanics are trivial to code up.

Let’s see how far I can go.

Design considerations

Reinforcement learning algorithms (Q, Sarsa) are usually represented as agent-controlled episodes, i.e., the agent performs actions in a loop, each time requesting a response from the outer environment. For multi-agent games, it becomes useful to have the loop controlled by the environment, so that at every game step, a player/agent is called upon to choose an action (each agent possibly using its own algorithm). The RL algorithm is therefore turned inside-out. This may be a relatively minor refactoring but is a useful new way to visualize the algorithm.

Moreover, since historical episodes need to be replayed at the end of every epoch (in order to generate updated training data for the FA), it becomes useful to separate an RL algorithm into an “action” component and a “learning” component. The “action” component simply plays actions based on the current policy (and FA values) while allowing for sufficient exploration. The steps thereby taken in the episode – plus all the older historical episodes – can later be fed through the “learning” component to generate target values for training data that will be used to update the FA.

Exploration

In the racecar project, I kept track of the number of visits to every state, and used that number to adjust the epsilon probability of random exploration from that state. In Connect-4 however, there are simply too many states to keep track of.

Although there are other very interesting approaches to exploration that could avoid the need for counters, I wanted to use the same familiar approach for now.

My first insight was that I could calculate a weight (a probability of exploration) for each feature separately, and multiply those weights together to get a final epsilon value. So, the more the number of features in the current state that are insuficently explored, the higher the likelihood of exploration. This would dramatically decrease the number of counters I would need (just 1 for each feature). Moreover this trick seems intuitively very similar to the way function approximators use features instead of states!

However, this may not work very well if I used the naive simplistic approach. I was planning on using each gridpoint in the 7×6 space as a feature – each valued as one of: “empty” or “my coin” or “opponent coin” (0, 1 or -1). If we calculated exploration probability on a per-gridpoint basis, one could imagine that we’d end up over time with every gridpoint being equally explored (⅓ for each of the three values), and not offering any real sense of whether a particular permutation of the board has been explored before or not. The naive approach essentially treats features as being mutually independent when in reality they are not.

On the other hand, if I pooled gridpoints together into various small groups, and kept track of the visit-counts of every possible permutation within each group, that might provide a better sense of whether the overall board state has been explored. For instance, we could have all gridpoints in a single row be one group, or better yet, we could have locally adjacent gridpoints grouped together since, intuitively, adjacency matters a lot in a game like Connect-4.

Function approximator

When I first started thinking about applying RL to “thinking” games like Connect-4, I couldn’t decide which component was responsible for capturing the thinking / lookahead logic — was it the explorative RL algorithm (such as Sarsa or Q(λ)) or the Function Approximator (such as a NN or Random forest). It seemed like the exploration algorithm was merely responsible for exploring the space well enough to generate good training data for the FA. But that the FA in turn was merely responsible for returning a “goodness value” for a certain snapshot of the game-state. 

It seemed like the Function Approximator was merely responsible for predicting a “goodness value” for a certain snapshot of the game-state – it would output a “hunch” for the current state – without thinking about the future at all. If someone were at all responsible for traversing game states sequentially, it could only be the RL exploration algorithm – but the RL algorithm certainly didn’t attempt to peek into the future, it only collected experience from paths traversed in the past.

My guess right now is that I may be selling FAs short, that perhaps “hunches” are all that are needed here. E.g. could a chess grandmaster play a successful game against an average chess-player without any conscious thinking – with only instinctive hunches? I believe so! I believe that highly-experienced players develop intuitions for game situations that regular players normally analyse only with a lot of lookahead-thinking. I would certainly be happy with such an expert RL agent if this were true! To answer my question on whose responsibility it is, I think it would be a joint task — the FA’s responsibility is to model gameplay patterns in the historical data that is collected by the exploration algorithm. Would a FA truly be capable of modeling this information? Or am I just being too optimistic about neural network magic? That remains to be seen.

One specific consideration for the FA in boardgames like Connect-4, is that the features are laid out in a two-dimensional space, and since this two-dimensional structure matters a lot in evaluating the value of a given state, we could/should take advantage of this a-priori structure. Specifically, I suspect that convolutional neural networks (CNN) will play an important role here.

Data augmentation

A simple way to double the amount of training data, is for every board state to be mirrored horizontally, i.e. a left-right flip, including the action (chosen column). The earned rewards and expected FA values should apply equally to both states.

In addition to having the agent gather and analyze its own episode history, we can also have it borrow and analyze the opponent’s episode history as if it were its own. Beyond just doubling the amount of training data, this approach would also make up for some gaps: (a) the agent’s history consists mainly of losses – rarely of wins, (b) the agent’s history (in my implementation) involves always playing first, so the board would always contain an even number of coins.

Training and results

TLDR; As of now, the RL system is up and running but I still haven’t gotten very satisfying results. The agent is able to win games against simple opponents but I suspect its learning is only at a superficial level. I need to explore many more neural network architectures before I can land on something with great results.

My overall strategy for training the RL agent was to make it compete against progressively harder opponents. It is quite trivial to write a “lookahead” player that can recursively explore future paths up to a depth D. Increasing the depth D can give us opponents with increasing strength.

I first tried training the RL agent against an opponent that played randomly (D = 0). It didn’t take long for the RL agent to learn overly-simple strategies to win, e.g. “always play column 6” – which would be sufficient to win a majority of the games. Indeed, the average number of turns needed to win was around 8 (i.e., quite minimal). Interestingly, the agent always settled on just one or two preferred actions (e.g. just columns “6” or “3”) and didn’t bother much with other potentially winning columns.

I next trained the RL agent against an opponent that looked ahead 1 step (D = 1), i.e., if the opponent saw a move that could be an immediate win, it would always play that move. Understandly, this agent is not much more effective than the random agent, since it would have to first serendipitously line up 3 coins in a line. My RL agent was able to outwit this agent almost as easily as the random-playing agent.

I had a harder time with a D = 2 lookahead opponent. This opponent would always play to prevent the RL agent from being able to win in the immediate next move. So the RL agent’s simplistic strategies can no longer work. I had to finally bring out the convolutional layers in addition to the fully-connected layers. Now, during training, the “average number of moves before agent loses” kept increasing gradually, until  – around 12000 games into it – the agent started breaking even in the wins vs losses, and later started winning.

I spent the rest of the time struggling with a D = 3 opponent. This opponent can identify if a potential move can guarantee a win in its next move. This training was hard enough that it surfaced a lot of issues in my algorithm and forced me to plot various graphs for analysis. I was also beginning to worry that my earlier successes were due entirely to exhaustive exploration, and I needed tools to discount that possibility. I describe most of these issues below in the Notes section.

So this is only the first stage of the project. The next stage, the harder one, is to figure out the right function approximator or neural network architecture to capture the intuitions needed (assuming of course that such an architecture exists!) To be continued…

Notes and Insights

• Measuring performance: A straightforward approach to measuring the performance of an agent is to simply have it play N new games against an opponent and to compute a score (e.g., weighting quicker wins as better than slower wins.). This could be done at the end of every epoch, for example, and it’s a useful measure. It’s what we ultimately care about the most.
  However, is it possible to track a validation score during training itself?
  • Validation during NN training: In the normal sense of a “validation set”, I split the NN’s input dataset (each row consisting of <state,action>→target pairs) into a validation and training dataset. I set aside the validation set and used it for measurement only. I got something like this:
    Note that the splitting of the input dataset into validation and training happens at the start of every epoch, so they both start with the same cost performance.
    Within the context of training a single update of the NN, this validation plot is just fine. In some sense, validation testing is all about the NN and whether the training pass is going well. Besides, the “input dataset” coming in at every epoch is different from the last, because the target values have all been recomputed (by the Q / Sarsa algorithm.)
    Yet, it’s problematic. What we really want to know is whether our training of the RL agent is going well, whether the agent is learning anything at all – and specifically, how well its predictions might match that of a so-far-unseen episode!
    Moreover, going from epoch to epoch, what was once a validation datapoint may now be picked as a training datapoint – or vice-versa (with targets shifted perhaps only a little bit since the last time). Over time, we end up “training” the entire validation set! This defeats the purpose.
  • Validation across the whole RL process: Instead of partitioning validation data at the NN-input level, I now partition it at the episode history level, i.e., I set aside whole games into a “validation history” set separate from a “training history” set. I generate targets for each of these sets (using Q/Sarsa) and use only the latter for training and save the former for validation purposes at NN training time. Now we get a plot like this:
    
    This gives us a much clearer idea of what’s happening. Validation cost is growing and moving away from training cost, which is approaching zero.
  • Duplicate data in RL: It seems to me that in RL, there is a high likelihood of duplicate data being generated purely randomly, e.g. in the lower levels of the “lookahead tree.” Should we try to avoid training on a duplicate datapoint if it already exists in the validation set? Should we only use “rare” states (low exploration score) into the validation set? I don’t see any obvious answers to these questions. Consider the extreme case — that the game tree has been fully explored and fully memorized by the NN! — is that a bad thing or a good thing??
• Regularization: To be honest, I don’t yet know what’s going on here. Applying a non-zero regularization constant didn’t seem to help much – the validation cost still appears to race upwards at the start of every epoch – and sometimes regularization made things worse than they were! On the other hand, as I sometimes saw (fig. on right), even without regularization, validation costs stayed low as long as there was a ton of data for training. (“More Data is always the best regularizer”? Or is this just caused by duplicate datapoints residing in both the validation and training sets?)
• Focusing on a single epoch for NN training: In the early stages, I wanted to find usable hyperparameters for NN training that I could then simply plug in. So I first ran a lot of games/episodes, fed them through Q(λ) processing to generate (just okay) target values, and stored the training data to a file. I could then easily play around with the NN hyperparameters, directly using the training data from disk.
  Unfortunately, no magic was witnessed in this process. The data was memorized superficially (to the extent possible) and then it stayed flat. NN wrangling will have to come later.
• Coordinate descent: We’re familiar with the idea that in gradient descent, there is a gradual decay in cost, i.e. a gradual convergence of the NN weights towards their final values. But what about the target values for an RL algorithm like Q(λ) — do these too converge over time?
  
  In the beginning, I was getting these weird error cost graphs (fig. on right).
  Why would the error cost jump up at every epoch? Was it caused by the newer episodes introducing conflicting target values? (Not really.) Would it eventually flatten out? (Not really.) Was it the inability of the NN to generalize the data? (Perhaps?) Frustratingly, in some cases I even saw the training cost go above the validation cost!And later on (after I’d made some other changes to the NN) I started seeing the opposite problem – the error cost was dropping for no reason at all! Running the algorithm with a very high regularization constant (not much learning occurring) and no new incoming data (learning only on existing history), I was seeing a step-down graph (fig. on right). I was at a loss to explain how the RL algorithm could possibly reduce errors with negligible help from the NN.
  (I further verified that the drop was happening before the NN training had started.) My hypothesis was that the Q(λ) algorithm took time before it could “see into the future” because the eligibility trace was of limited length, depending on the lambda value and other factors. Unfortunately though, changing the lambda value had little effect on this graph.

  But I was close! Stepping through the code finally reminded me of how this algorithm works. In essence, what we have here is a coordinate descent between the NN’s optimizer and the Q(λ)’s target-value updates. During a NN update, the outputs shift closer to the target values. Then, during a Q(λ) update, the targets move closer to [a computed value that’s based on] the outputs.
  So if, at the start of a new epoch, we see the loss drop down considerably even before the FA updates itself, it implies that the (existing) FA had already anticipated this  incoming data (even before the data had been generated/updated by Q(λ))! This suggests that the FA is learning and generalizing well.

  What was tripping me up for a long time was that it seemed impossible that a newly updated target value could be any closer to the FA’s intuitions than the state’s current value – that was just output by the FA itself! However, my mistake was in assuming that the FA’s output for a given state was exactly the state’s previous target value. This is usually not the case because the FA update merely tries to fit to the target as well as it can – it perhaps hasn’t had enough iterations yet. Worse, although the FA update decreases the overall loss, there may be several data points whose loss actually increases instead.

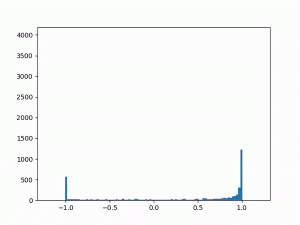
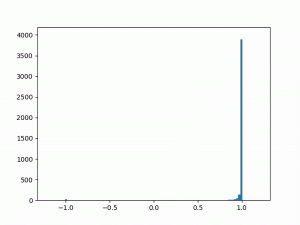
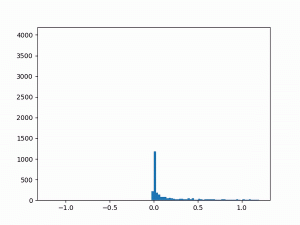
• Difficulty training on positive paths: As learning progresses, the average delta between the target and the current value naturally decreases (assuming no new episodes). However, I noticed that although the average delta for the episodes played by the agent went steadily down to zero, the average delta for the episodes played by the opponent refused to go below around 0.24. I struggled to gain insights from the statistics numbers (mean and variance) and so finally plotted histograms for the distributions (current value, target value and delta) which was now more revealing:

  

  

  

  The above shows the histograms for the opponent’s episode data. We can see in the current value histogram on the left that there is a ‘lump’ of datapoints (near -0.8) that has not yet successfully moved all the way to +1 on the right. It seems like the NN needs more time to learn those datapoints – and that’s okay.

  But why should this lump exist only for opponent episodes, and not for the agent’s own? Does it have something to do with the opponent having way more winning episodes (each resulting in positive rewards) than the agent?

  Diving deeper into some of those poorly-learned datapoints, it’s clear that the problem here arises when a state reaches out to the next state in order to find a “max action value” – and gets a max value which is way higher than it should be – e.g. when all the “next actions” offer values near -0.65 except for one action that offers a high +0.95 value for no plausible reason. (Why might this happen? Perhaps the NN is simply not yet ready to output consistent results.) In other words, a single errant prediction can completely throw off the computation, thanks to the “max” operator in the Q(λ) algorithm.

  Why would this be more of an issue for episodes of the opponent specifically? With more positive targets to train for, it’s likely that these episodes cause the NN to lean more towards positive outputs in general, making it easier to get one wrong. The “max” operator makes such mistakes unforgivable. I suspect that the Sarsa algorithm may therefore not face the same problem.

• Source code on github

Conclusion

In this episode, I worked my way through most of the RL plumbing for 2-player games and analyzed the interesting behaviors and graphs of the overall system. I was only just able to train an agent that could play successfully against a D=3 look-ahead agent.

A major chunk of the work still remains to be done for the function approximator – getting the right NN architecture and fine-tuning it. That would pave the way forward for a truly powerful Connect-4 agent.